题目

最佳调度问题

问题描述

设有n个任务由k个可并行工作的机器来完成，完成任务i需要时间为ti。试设计一个算法找出完成这n个任务的最佳调度，使完成全部任务的时间最早。（要求给出调度方案）

完成全部任务的时间为运行时间最长的机器上运行的总时间，所有机器都是相同的。一个任务只能在一个机器上完成，且在完成之前不会被其他任务抢占。

算法设计

回溯法

回溯法是一个既带有系统性又带有跳跃性的搜索算法。

• 系统性：它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。

• 跳跃性：算法搜索至解空间树的任一结点时，判断该结点为根的子树是否包含问题的解，如果肯定不包含，则跳过以该结点为根的子树的搜索，逐层向其祖先结点回溯。否则，进入该子树，继续按深度优先的策略进行搜索。

这种以深度优先的方式系统地搜索问题的解的算法称为回溯法，它适用于解一些组合数较大的问题。

提高回溯法效率的二种方法

• 用约束函数剪去不满足约束的子树；

• 用限界函数剪去不能得到最优解的子树。

最佳调度问题可以用回溯法解决，并且是属于子集树回溯法。对于每个任务i，都可能分配到k台机器的任意一台上，解空间为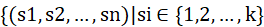，现在要求的是使得最长机器时间最短的解。

回溯算法伪代码如下：

BackTrack(int task,int spendtime){
    if (task == n){ //分配完毕
        if(spendtime < besttime){
            besttime = spendtime;
            记下当前最优解的方案;
        }
        return ;
    }
    for(每台机器j){
        将任务task分配给当前机器j;
        机器j的时间 += 任务task的时间;
        BackTrack(task + 1,max(spendtime,机器j的时间));
        回溯，不将任务task分配给当前机器j，用0表示未分配;
        机器j的时间 -= 任务task的时间;
    }
    return ;
}

初始时调用BackTrack(1,0);

如果只是简单的回溯，解空间随着n和k的增大呈指数级增长，时间复杂度达O(k^n)，为此，这里进行了几处优化：

• 最优化剪枝——如果当前各个机器时间中的最长时间，即spendtime已经大于最佳方案的时间（besttime），则不再继续向下一层搜索。

• 初始解——使用贪心的方法求得一个初始解，即得到一个初始的besttime，这样可以让besttime尽快地减少至接近最后的结果，使得上面的剪枝能更早地抛弃不需要的子树。贪心的策略是，每次分配当前任务都选择最短时间的机器。

• 预排序——初始时，任务按时间降序排列，即从时间最长的任务开始分配，这样可以加强上面的剪枝，减少不必要的搜索层次

• 去除重复的搜索——由于机器之间是无差别的，而一台机器分配的任务也是无序的。对于某个方案，对所有机器进行重新排列，以及对一台机器的任务重新排列，得到的任意一个方案对于这个问题都是等价的（最佳调度时间相同）。因此，搜索时，只考虑按每台机器的最长的任务的时间降序排列的那种方案。由于任务分配前已按时间降序排列，故放入一台空机器的第一个任务就是该机器的最长时间的任务。如果当前要放入一台空机器的任务时间大于前一台机器的最长任务的时间就说明情况重复了，不用继续搜索。

代码

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#define MAXTASK 100           //最大任务数
#define MAXMACHINE 100          //最大机器数
using namespace std;
int n,k;                    //n：任务数，k:机器数
int times[MAXTASK];         //每个任务对应的时间
int schedule[MAXTASK];      //当前调度方案，每个任务分配的机器号，取0表示还未分配
int machinetime[MAXMACHINE] = {};    //每个机器工作的总时间,机器下标从1开始算
int machinemaxtasktime[MAXMACHINE] = {};

int besttime = 999999999;     //最优解，即完成全部任务最短时间，初始化为无穷大
int bestschedule[MAXTASK];   //最优解的调度方案
int max(int a,int b){
    return a > b ? a : b;
}
bool cmp(int a,int b) {
    return a > b;
}
int init(){//贪心地求出初始解
    int tmpmachinetime[MAXMACHINE]={};
    int minmachine,mintime = 999999999;
    int spendtime = 0;
    for(int i = 1;i <= k;i++){
        tmpmachinetime[i] = times[i];//前k个任务分配给k个机器
    }
    for(int i = k + 1;i <= n;i++){
        for(int j = 1;j <= k;j++){
            if(tmpmachinetime[j] < mintime){
                mintime = tmpmachinetime[j];
                minmachine = j;
            }
        }
        tmpmachinetime[minmachine] += times[i];
        spendtime = max(spendtime,tmpmachinetime[minmachine]);
    }
    return spendtime;
}
void BackTrack(int task,int spendtime){ //子集树回溯法
    if (task == n){ //分配完毕
        if(spendtime < besttime){           //可行解与当前最优解进行比较
            besttime = spendtime;
            for(int i = 0;i < n;i++) //记下当前最优解的方案
                bestschedule[i] = schedule[i];
        }
        return ;
    }
    for(int j = 1;j <= k;j++){
        if(max(spendtime,machinetime[j] + times[task]) < besttime){
        //剪枝，若当前最长机器时间已经超出最少时间，则不继续搜索
            if(machinetime[j] == 0){//当前机器是空的
                if(machinemaxtasktime[j - 1] < times[task])
                    break;
                    //对于一个可行解对应的方案，把各个机器重新排序，是等价的
                    //故我们只保留按每台机器最长任务的时间降序的方案
                    //由于任务分配前按时间降序排列，放入一台空机器的第一个任务就是该机器的最长时间的任务
                    //如果当前要放入一台空机器的任务时间大于前一个机器的最长任务的时间
                    //说明情况重复了
                machinemaxtasktime[j] = times[task];
            }
            schedule[task] = j;          //将任务t分配给当前机器j
            machinetime[j] += times[task];
            BackTrack(task + 1,max(spendtime,machinetime[j]));
            schedule[task] = 0;         //回溯，不将任务t分配给当前机器j，0表示未分配
            machinetime[j] -= times[task];
            if(machinetime[j] == 0) //恢复
                machinemaxtasktime[j] = 0;
        }
    }
    return ;
}
int main(){
    FILE *fp = fopen("in3.txt","r");
    fscanf(fp,"%d%d",&n,&k);
    for(int i = 0;i < n;i++){
        fscanf(fp,"%d",&times[i]);
    }
    fclose(fp);

    sort(times,times + n,cmp); //times按降序排序
    besttime = init();
    machinemaxtasktime[0] = 999999999;

    printf("----------------------------Input----------------------------\n");
    printf("Task Time\n");
    for(int i = 0;i < n;i++)
        printf("%4d %4d\n",i,times[i]);

    BackTrack(0,0);       //子集树回溯法

    printf("----------------------------Output----------------------------\n");
    printf("Best time: %d\n",besttime);
    printf("Task Machine\n");  //按任务对应的机器输出
    for(int i = 0;i < n;i++)
        printf("%4d %4d\n",i,bestschedule[i]);
    printf("Machine  Task_list\n"); //按机器对应的任务输出
    int tmp[MAXMACHINE][MAXTASK]={}; //第一维为机器下标，第二维第0个为任务数，之后为任务下标列表
    for(int i = 0;i < n;i++){ //i为任务下标
        int j = bestschedule[i]; //该任务对应的机器下标
        int l = ++tmp[j][0]; //当前机器分配的任务数+1
        tmp[j][l] = i;
    }
    for(int j = 1;j <= k;j++){
        printf("%4d    ",j);
        for(int i = 1;i <= tmp[j][0];i++)
            printf("%4d",tmp[j][i]);
        printf("\n");
    }
    return 0;
}