题目
红黑树维护算法及其区间树应用
算法设计
(一)红黑树
红黑树是一棵二叉搜索树,是众多平衡二叉树中的一种,它可以保证在最坏情况下基本操作的时间复杂度为O(lgn)
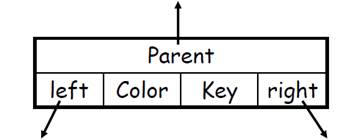
红黑树的每个结点包含5个属性:color、key、left、right、parent,分别表示颜色、关键字、左孩子、右孩子、父亲。
红黑树有以下性质:
① 每个节点必须为红色或黑色;
② 根为黑色;
③ 树中的nil叶子为黑;
④ 若节点为红,则其两个孩子必为黑;
⑤ 每节点到其后代叶子的所有路径含有同样多的黑节点;
红黑树的基本操作:
(1)左旋/右旋
这是一种能保持二叉搜索树性质的局部操作。

以左旋为例,操作顺序如下:
① y←right[x] //记录指向y节点的指针
② right[x]←left[y], p[left[y]]←x //β连到x右
③ parent[y]←parent[x], parent[x]的左或右指针指向y //y连到p[x]
④ left[y]←x, parent[x]←y// x连到y左
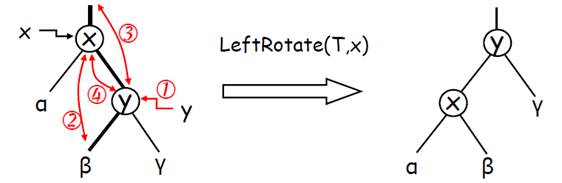
该操作的时间复杂度T(n)=O(1)
(2)插入
这个操作是在二叉搜索树的插入操作上略作修改,分为三步:
①将z节点按BST树规则插入红黑树中,z是叶子节点;
②将z涂红;
③调整使其满足红黑树的性质;
调整过程分析如下:
Z插入之后,为红色结点,其两个孩子为黑色NIL,满足性质1,3,5,可能违反性质2,4,即z是(红色)根或者z的父亲是红色。
调整方案:通过旋转和改变颜色,自下而上调整(z进行上溯),使树满足红黑树性质。
(1)若z为根,将其涂黑;
(2)若z为非根,则p[z]存在
①若p[z]为黑,无需调整
②若p[z]为红,违反性质4,则需调整
具体来说分为6种情况:
case1~3为z的双亲p[z]是其祖父p[p[z]]的左孩子,*
case46为z的双亲p[z]是其祖父p[p[z]]的右孩子(与case13对称)。*
- Case1: z的叔叔y是红色,这时通过调整叔叔、父亲和祖父的颜色,将违反性质的结点上移,调整最多至根。若红色传播到根,将根涂黑,则树的黑高增1
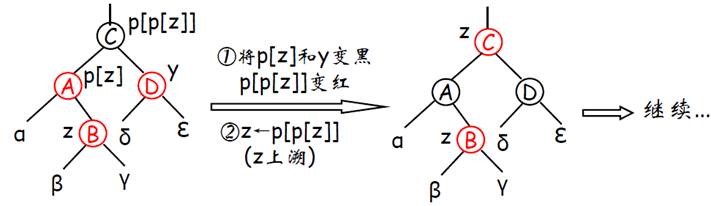
Case 2:当z的叔叔y是黑色,且z是双亲p[z]的右孩子,这种情况通过左旋变换为Case3.
Case 3:当z的叔叔y是黑色,且z是双亲p[z]的左孩子
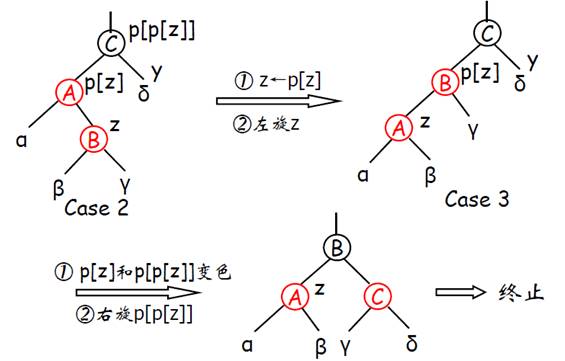
调整算法的时间:O(logn)
整个插入算法的时间:O(logn)
(3)删除
这个操作将树上的一个结点z删除,然后进行z的孩子的调整,使之满足二叉搜索树的性质,最后,然后红黑树性质被破坏,则需要进行颜色的调整。
首先是对删除结点z进行分类讨论,有3种情况:
Case 1:z为叶子;
Case 2:z只有一个孩子(非空)
case 1是case 2的特例,处理模式是一样
处理方式:删除z,连接x。这里x是z的中序后继;
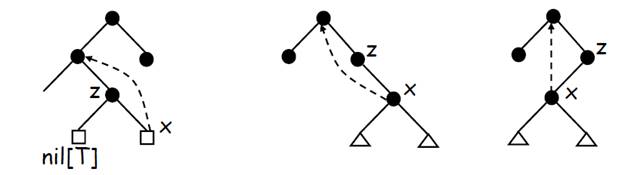
- Case 3:z的两个孩子均非空;
处理方式:
(1)找z的中序后继即找z的右子树中最左下节点y;
(2)删除y,将y的内容copy到z,再将y的右子连到p[y]左下。
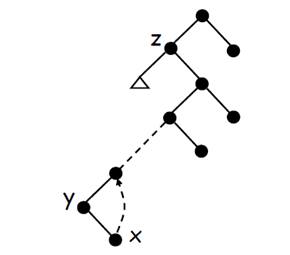
最后分析颜色的调整:
删红点不影响,删黑点需要调整。
对于结点x,或是y的唯一孩子,或是哨兵nil[T]。
可以想象将y的黑色涂到x上,于是
① 若x是根,且原为黑,直接移去多余一层黑色(树黑高减1),终止;
② 若x原为红,将y的黑色涂到x上,终止;
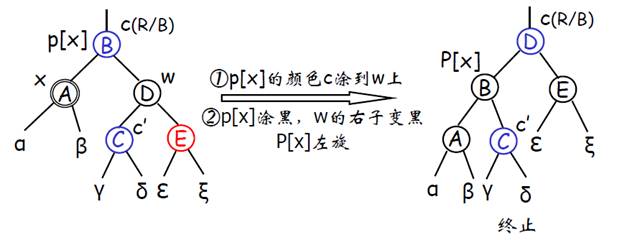
③ 若x非根节点,且原为黑色,则x为双黑。通过变色、旋转使多余黑色向上传播,直到某个红色节点或传到根;
具体来说,分为8种情况,
case 1~4为x是p[x]的左子;*
case 5~8为x是p[x]的右子(对称地)*
以case1~4为例
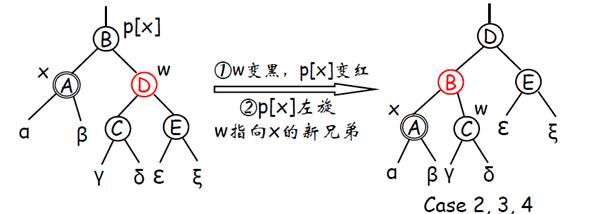
- Case 1:x的兄弟w是红色(w是红,则 p[x]必黑)
处理方式如图,目标是将情况变成Case2,3,4处理
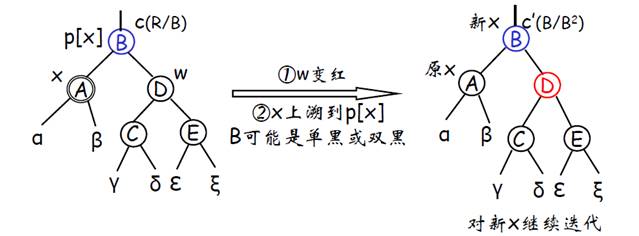
- Case 2:x的黑兄弟w的两个孩子均为黑
处理方式如图,目标是将 x上移到B,通过A和D的黑色上移
- Case 3:x的黑兄弟w的右子为黑且左子为红
处理方式如图,目标是将case3转为case4
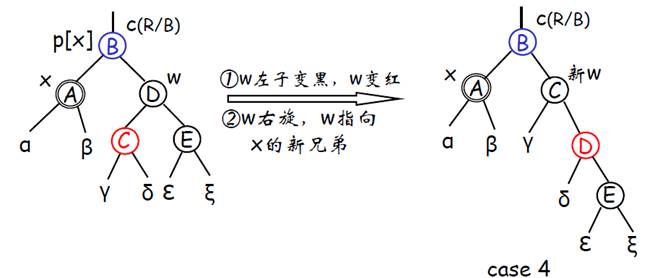
- Case 4:x的黑兄弟w的右子为红(左子为黑或红)
x的黑色上移给B,B的原色下移给D,D将黑色下移给C和E,通过旋转解决矛盾点C
(二)区间树
区间树是对红黑树的扩张,其每个结点存储一个区间,包括low和high两个值,其中low作为红黑树的key。
为了实现重叠区间的查找,还需要为每个结点添加一个max域,其值为以该结点为根的子树的所有区间的最大端点。
(1)max值的计算:该节点的区间右端点、左子树max值、右子树max值三者中的最大值。
max值的维护:需要在旋转、插入和删除时进行调整。
①左旋后,y的max更新为x原来的max,x的max重新按上面的方法计算,时间复杂度为O(1)。

②插入z时,z的max值设为自己区间的右端点,然后对于从根到插入位置的每个结点,如果其max值小于z的max值,则更新为z的max值。时间复杂度为O(logn)。
③删除z时,如果z只有一个孩子或者没有孩子,则直接从z的父亲开始向上到根结点,依次重新计算max值。如z有左右孩子,在找到z的中序遍历后继y后,从y的父亲开始向上至根结点,依次计算max值。时间复杂度为O(logn)。
(2)重叠区间的查找:x从根结点开始,如果x为nil或待查找的区间与其重叠,则返回x。否则,x更新,如果x左孩子不为nil且max值大于待查找区间的左端点,则x更新为x的左孩子,反之更新为x的右孩子。
时间复杂度为O(logn)
代码
#include <cstdio>
#include <cstdlib>
enum Color{
RED,
BLACK
};
typedef struct RBTreeNode{
struct RBTreeNode *parent;
struct RBTreeNode *left;
struct RBTreeNode *right;
Color color;
int key;//low
int high;//high
int maxep;//子树中区间最大端点
}node;
class RBTree{
public:
RBTree();
~RBTree();
struct RBTreeNode *root;
struct RBTreeNode *nil;
void Insert(node *z);
void Delete(node *z);
node* Search(int key);
node* IntervalSearch(int low,int high);
void Print();
bool Overlap(int alow,int ahigh,int blow,int bhigh);
void pn(node *x);
private:
void Updatemaxep(node *x);
void Updatemaxep2(node *x);
void _Print(node *x,int depth);
void LRotate(node *x);
void RRotate(node *x);
void Insert_fixup(node *z);
void Transplant(node *u,node *v);
node *Minimum(node *x);
void Delete_fixup(node *x);
};
int max(int a,int b){
if(a > b) return a;
else return b;
}
RBTree::RBTree(){
this->nil = new node;
this->nil->color = BLACK;
this->nil->left = NULL;
this->nil->right = NULL;
this->nil->parent = NULL;
this->nil->key = -1;
this->nil->high = -1;
this->nil->maxep = -1;
this->root = this->nil;
}
RBTree::~RBTree(){
delete this->nil;
}
void RBTree::Updatemaxep(node *x){
x->maxep = max(x->high,max(x->left->maxep,x->right->maxep));
}
void RBTree::LRotate(node *x){//左旋
node *y = x->right;
x->right = y->left;
if(y->left != this->nil)
y->left->parent = x;
y->parent = x->parent;
if(x->parent == this->nil)
this->root = y;
else if(x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
y->left = x;
x->parent = y;
y->maxep = x->maxep;//区间树维护maxep
Updatemaxep(x);//区间树维护maxep
}
void RBTree::RRotate(node *x){//右旋
node *y = x->left;
x->left = y->right;
if(y->right != this->nil)
y->right->parent = x;
y->parent = x->parent;
if(x->parent == this->nil)
this->root = y;
else if(x == x->parent->right)
x->parent->right = y;
else
x->parent->left = y;
y->right = x;
x->parent = y;
y->maxep = x->maxep;//区间树维护maxep
Updatemaxep(x);//区间树维护maxep
}
void RBTree::Insert_fixup(node *z){//插入后为保存红黑树性质而作的调整
while(z->parent->color == RED){ //父亲是黑则无需调整,父亲是红也保证了父亲存在(不是nil),并且祖父存在
if(z->parent == z->parent->parent->left){//父亲是祖父的左孩子
node *y = z->parent->parent->right;//记录叔节点
if(y->color == RED){//叔是红
z->parent->color = BLACK;//父亲变黑
y->color = BLACK;//叔变黑
z->parent->parent->color = RED;//祖父变红
z = z->parent->parent;//问题向上转移两层
}
else if(z == z->parent->right){//叔是黑
//z是父亲的右孩子,则对z父亲左旋,并且新的z是原来z的父亲,且是原来z的左孩子,统一按下面的情况处理
z = z->parent;
LRotate(z);
}
else{
z->parent->color = BLACK;//父变黑
z->parent->parent->color = RED;//祖变红
RRotate(z->parent->parent);//把黑色父亲旋转到祖父的位置,此时红左孩还是左孩,红祖父变成右孩子
}
}
else{//对称情况,父亲是祖父的右孩子
node *y = z->parent->parent->left;//记录叔节点
if(y->color == RED){//叔是红
z->parent->color = BLACK;//父亲变黑
y->color = BLACK;//叔变黑
z->parent->parent->color = RED;//祖父变红
z = z->parent->parent;//问题向上转移两层
}
else if(z == z->parent->left){//z是父亲的左孩子,则对z父亲右旋,并且新的z是原来z的父亲,且是原来z的右孩子,统一按下面的情况处理
z = z->parent;
RRotate(z);
}
else{
z->parent->color = BLACK;//父变黑
z->parent->parent->color = RED;//祖变红
LRotate(z->parent->parent);//把黑色父亲旋转到祖父的位置,此时红右孩还是右孩,红祖父变成左孩子
}
}
}
this->root->color = BLACK;
}
void RBTree::Insert(node *z){//插入
node *y = this->nil;
node *x = this->root;
z->left = this->nil;
z->right = this->nil;
z->color = RED;
z->maxep = z->high;//区间树维护maxep
while(x != this->nil){
x->maxep = max(x->maxep,z->maxep);//区间树维护maxep,从根到z的路径上的节点更新maxep
y = x;
if(z->key < x->key)
x = x->left;
else
x = x->right;
}
z->parent = y;
if(y == this->nil)
this->root = z;
else if(z->key < y->key)
y->left = z;
else
y->right = z;
Insert_fixup(z);
}
node* RBTree::Minimum(node *x){//以x为根的子树中的最小key的节点
while(x->left != this->nil)
x = x->left;
return x;
}
void RBTree::Transplant(node *u,node *v){//以v代替u,这里没有处理u和v的孩子,注意:u/v各自的指向结点并没有改变
if(u->parent == this->nil)//u是根
this->root = v;
else if(u == u->parent->left)
u->parent->left = v;
else
u->parent->right = v;
v->parent = u->parent;
}
void RBTree::pn(node *x){
printf("[%d,%d]|%d(%s)\n",x->key,x->high,x->maxep,x->color==RED?"R":"B");
}
void RBTree::Delete_fixup(node *x){
while(x != this->root && x->color == BLACK){
if(x == x->parent->left){
node *w = x->parent->right;
if(w->color == RED){
w->color = BLACK;
x->parent->color = RED;
LRotate(x->parent);
w = x->parent->right;
}
if(w->left->color == BLACK && w->right->color == BLACK){
w->color = RED;
x = x->parent;
}
else{
if(w->right->color == BLACK){
w->left->color = BLACK;
w->color = RED;
RRotate(w);
w = x->parent->right;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->right->color = BLACK;
LRotate(x->parent);
x = this->root;
}
}
else{//x == x->parent->right
node *w = x->parent->left;
if(w->color == RED){
w->color = BLACK;
x->parent->color = RED;
RRotate(x->parent);
w = x->parent->left;
}
if(w->right->color == BLACK && w->left->color == BLACK){
w->color = RED;
x = x->parent;
}
else{
if(w->left->color == BLACK){
w->right->color = BLACK;
w->color = RED;
LRotate(w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->left->color = BLACK;
RRotate(x->parent);
x = this->root;
}
}
}
x->color = BLACK;
}
void RBTree::Updatemaxep2(node *x){
while(x != this->nil){
Updatemaxep(x);
x=x->parent;
}
}
void RBTree::Delete(node *z){
node *x;
node *y = z;
Color y_original_color = y->color;
if(z->left == this->nil){//没有左孩子或者没有孩子
x = z->right;//可能是空
Transplant(z,z->right);
Updatemaxep2(z->parent);
}
else if(z->right == this->nil){//没有右孩子但有左孩子
x = z->left;
Transplant(z,z->left);
Updatemaxep2(z->parent);
}//上面两种情况,直接删除z,以z的一个孩子代替z
else{//有左右孩子
y = Minimum(z->right);//寻找z在中序遍历中的下一个结点,以此为新的y,并且y没有左孩子
y_original_color = y->color;
node *g = y->parent;
x = y->right;
if(y->parent == z){//y的父亲是z,则y就是z的右孩子
x->parent = y;
}
else{//y是z的右子树中最小者,但不是z的右孩子
//if(y->right != this->nil)
Transplant(y,y->right);
y->right = z->right;
y->right->parent = y;
}
Transplant(z,y);//用y代替z
y->left = z->left;
y->left->parent = y;
y->color = z->color;
Updatemaxep2(g);
}
if(y_original_color == BLACK)
Delete_fixup(x);
}
void RBTree::_Print(node *x,int depth){
if(x != this->nil){
_Print(x->right,depth+1);
for(int i = 0;i < depth - 1;i++){
printf(" ");
}
printf("[%d,%d]|%d(%s)\n",x->key,x->high,x->maxep,x->color==RED?"R":"B");
_Print(x->left,depth+1);
}
}
void RBTree::Print(){
node *p = this->root;
printf("------------------------------------------------------------------------------------\n");
_Print(this->root,1);
printf("------------------------------------------------------------------------------------\n");
}
node* RBTree::Search(int key){
node *x =this->root;
while(x != this->nil && key != x->key)
if(key < x->key)
x = x->left;
else
x = x->right;
return x;
}
bool RBTree::Overlap(int alow,int ahigh,int blow,int bhigh){
if(ahigh < blow || alow > bhigh) // a & b do not overlap
return 0;
return 1;
}
node* RBTree::IntervalSearch(int low,int high){
node *x=this->root;
while(x != this->nil && !Overlap(low,high,x->key,x->high))
{
if(x->left != this->nil && x->left->maxep >= low)
x = x->left;
else
x = x->right;
}
return x;
}
int main(){
int sel;
int i,n;
char path[128] = "in2.txt";
int low,high;
node *tmpnode;
RBTree *T = new RBTree();
while(1){
printf("MENU:\n1-File\n2-Insert\n3-Delete\n4-Find\n5-Print\n6-Exit\nSel:");
scanf("%d",&sel);
switch(sel){
case 1:{
//printf("Input file path:");
//scanf("%s",path);
FILE *fp=fopen(path,"r");
fscanf(fp,"%d",&n);
for(i=1;i<=n;i++){
node *p = new node;
fscanf(fp,"%d %d",&(p->key),&(p->high));
T->Insert(p);
T->Print();
}
fclose(fp);
break;
}
case 2:{
printf("Input low and high:");
scanf("%d%d",&low,&high);
node *p = new node;
p->key = low;
p->high = high;
T->Insert(p);
T->Print();
break;
}
case 3:{
printf("Input low:");
scanf("%d",&low);
if((tmpnode = T->Search(low)) == T->nil){
printf("can't find this node.\n");
break;
}
//printf("%d,%d,%d",tmpnode->key,tmpnode->high,tmpnode->maxep);
T->Delete(tmpnode);
T->Print();
break;
}
case 4:{
printf("Input low and high:");
scanf("%d%d",&low,&high);
if((tmpnode = T->IntervalSearch(low,high)) == T->nil)
printf("can't find.\n");
else printf("[%d,%d]\n",tmpnode->key,tmpnode->high);
break;
}
case 5:{
T->Print();
break;
}
case 6:{
return 0;
}
}
}
delete T;
return 0;
}
总结
这次实验让我比较深入地了解了红黑树的性质和操作及其应用。红黑树是高级数据结构,它可以保证在最坏情况下基本操作的时间复杂度为O(lgn),但编写的代码较为复杂,需要分清楚每种情况及其对应的处理,课本种对情况的分类十分精炼,有的情况不是并列的,不同的情况可能是相互转换的关系,需要仔细思考。