题目
求平面上n个顶点的最近点对问题
算法设计
分治法
1.先考虑一维的情形,即线段上最近点对。
用x轴上某个点m将S划分为2个子集S1和S2,使得S1={x∈S|x≤m};S2={x∈S|x>m},S1∪S2=S ,S1∩S2=Φ,则线段上最近点对为以下三者中的距离最小者:
(1)左半边S1的最近点对
(2)右半边S2的最近点对
(3)跨越分点m的最近点对
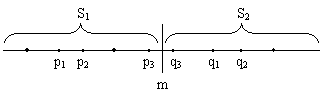
左半边S1的最近点对和右半边S2的最近点对的求解可以递归地调用该过程。而跨越分点m的最近点对,我们可以将S1中的一点与S2中的每一点计算距离,但这将花费O(n^2)。
事实上,通过求解左右两个子问题,我们已经得到一个当前最近点对的距离δ,在S1中,任何一个宽度为δ的区间内只分布着一个点,否则,存在两点距离小于δ,同理,S2中也是。因此,我们只需要考虑[m-δ,m+δ]区间内的点对距离,在[m-δ,m]如果有点,只能有一个点,这个点就是S1中距离m最近的点。区间[m,m+δ]同理。如果这两个点都存在,则计算距离,并与δ比较,因此,只需要O(n)时间完成问题的合并。
m点的选取问题:任意选取分割点m,有可能造成划分出的子集S1和S2的不平衡,最坏情况下有递归式:
T(n) = T(n-1) + O(n)
其解为T(n)=O(n^2)
如果我们恰当地选取m,是S1和S2中点的数量基本相同,则有递归式:
T(n) = 2T(n/2) + O(n)
其解为T(n)=O(nlogn)
为了选取m,我们可以事先对这些点排序,取m为下标中位数的点的坐标。
2. 考虑二维的情况,即本次实验求解的问题。
类似一维情况,将平面分为两个半平面,使两边各分布约一半的点,为了确定分割线x = m,先对所有点按x坐标进行排序,取m为下标中位数附近两个点的x的坐标的平均值。
递归地在S1和S2上解最接近点对问题,我们分别得到S1和S2中的最近点对的距离δ1和δ2。现设δ = min(δ1, δ2)。
现在考虑两个点分别在S1和S2中的情况。类似一维的情况,我们只需要考虑条带区域[m-δ,m]和[m,m+δ]中点对的距离,记这两个区域为P1和P2。
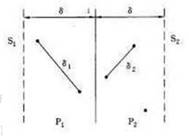
在一维的时候,距分割点距离为δ的2个区间P1[m-δ,m]和P2 [m,m+δ]中最多各有S中一个点,因而这两个点成为唯一的未检查过的最接近点对候选者。但在二维情况下,P1 [m-δ,m]中可能存在多个点,并且他们的距离大于δ,P2 [m,m+δ]同理。因此,最坏情况下,S1中的点可能都在P1 [m-δ,m]中,S2中的点可能都在P2 [m,m+δ]中,这样就需要花费O(n^2)来合并问题(检查跨越P1、P2的所有点对)。
事实上,我们不必检查如此多的点对,考虑P1中任意一点p,它若与P2中的点q构成最接近点对的候选者,则必有d(p,q)< δ。显然,这样的点只会分布在一个δ×2δ的矩形R中,如下图。
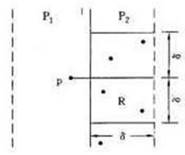
由δ的意义可知P2中任何2个S中的点的距离都不小于δ。我们可以将矩形R的长为2δ的边3等分,将它的长为δ的边2等分,形成6个(δ/2)×(2δ/3)的矩形。

若矩形R中有多于6个S中的点,则由抽屉原理易知至少有一个(δ/2)×(2δ/3)的小矩形中有2个以上S中的点。设a,b是这样2个点,它们位于同一小矩形中,则d(a,b)≤sqrt((δ/2)^2+(2δ/3)^2) <δ ,这与δ的意义相矛盾。
由此可以推出矩形R中最多只有6个S中的点,极端情形如下图。

因此,在分治法的合并步骤中,我们最多只需要检查6×n/2=3n对候选者,而不是O(n^2)对候选者。但这不意味着我们可以在O(n)时间内完成分治法的合并步骤。因为我们并不确切地知道要检查哪6个点。
为了解决这个问题,我们需要将P1和P2中的点分别按其y坐标排序,则对P1中每一点最多只要检查P2中排好序的相继6个点。排序花费的时间为O(nlogn)。这样得到递归式
T(n) = 2T(n/2) + O(nlogn)
其解为T(n) = O(nlognlogn)
一种改进的方法是,在最开始的时候,在按x排序后,然后确定完m的坐标后,对所有点按y坐标排序,这样就不用在递归函数中使用排序,合并问题的时间取决于检查跨P1、P2点对的时间O(n),有递归式
T(n) = 2T(n/2) + O(n)
其解为T(n) = O(nlogn)
代码
#include <cstdio>
#include <cstdlib>
#include <ctime>
#include <algorithm>
#define INF 99999999
#define MAX_DOT_NUM 100000
using namespace std;
typedef struct _dot{
double x;
double y;
}dot;
typedef struct _dpair{
double dis;
dot dota;
dot dotb;
}dpair;
int n;
dot *dots=new dot[MAX_DOT_NUM+1];
dpair dpairmin(dpair dp1,dpair dp2){
return dp1.dis<dp2.dis?dp1:dp2;
}
double distance(const dot &a,const dot &b){
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double cmp(const dot &a,const dot &b){
return a.x<b.x || a.x==b.x && a.y<b.y;
}
double cmpy(const dot &a,const dot &b){
return a.y<b.y;
}
dpair minDistance(int l,int h){
dpair tmpdp;
if(l==h){
tmpdp.dis=INF;
return tmpdp;
}
if(l==h-1){
tmpdp.dis=distance(dots[l],dots[h]);
tmpdp.dota=dots[l];
tmpdp.dotb=dots[h];
return tmpdp;
}
int m=(l+h)/2;
dpair dp1=minDistance(l,m);
dpair dp2=minDistance(m+1,h);
dpair dp=dpairmin(dp1,dp2);
dot *ldots=new dot[MAX_DOT_NUM/2+2];
dot *rdots=new dot[MAX_DOT_NUM/2+2];
double xm=(dots[m].x+dots[m+1].x)/2;
int k,i,nl,nr;
for(k=m;k>=l;k--){
if(dots[k].x>=xm-dp.dis)
ldots[m-k+1]=dots[k];
else
break;
}
nl=m-k;
sort(ldots+1,ldots+nl+1,cmpy);
for(i=m+1;i<=h;i++){
if(dots[i].x<=xm+dp.dis)
rdots[i-m]=dots[i];
else
break;
}
nr=i-m-1;
sort(rdots+1,rdots+nr+1,cmpy);
int istart=1;
for(k=1;k<=nl;k++){
for(i=istart;i<=nr;i++){
if(rdots[i].y-ldots[k].y<=dp.dis){
tmpdp.dis=distance(ldots[k],rdots[i]);
tmpdp.dota=ldots[k];
tmpdp.dotb=rdots[i];
dp=dpairmin(dp,tmpdp);
}
else{
istart=i-6<1?1:i-6;
break;
}
}
}
delete []ldots;
delete []rdots;
return dp;
}
int main(){
int sel;
int i;
char path[128];
srand(time(NULL));
printf("MENU:\n1-INPUT\n2-FILE\n3-RANDOM\n");
scanf("%d",&sel);
switch(sel){
case 1:{
printf("Input dots, the num of dots 'n' in first line, the next n lines are 'x' and 'y' for each dots.\n");
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%lf %lf",&(dots[i].x),&(dots[i].y));
break;
}
case 2:{
printf("Input file path, the data format is same as 1-INPUT.\nFile path:");
scanf("%s",path);
FILE *fp=fopen(path,"r");
fscanf(fp,"%d",&n);
for(i=1;i<=n;i++)
fscanf(fp,"%lf %lf",&(dots[i].x),&(dots[i].y));
fclose(fp);
break;
}
case 3:{
printf("Input n, the program will generate n dots randomly.\nn:");
scanf("%d",&n);
for(i=1;i<=n;i++){
dots[i].x=rand()%100;
dots[i].y=rand()%100;
}
break;
}
}
sort(dots+1,dots+n+1,cmp);
dpair dp=minDistance(1,n);
printf("(%lf,%lf) and (%lf,%lf) is dot pair with the min distance: %lf.",dp.dota.x,dp.dota.y,dp.dotb.x,dp.dotb.y,dp.dis);
return 0;
}